Boost.Asio
简单来说,Boost.Asio是一个跨平台的c++网络和I/O库,使用它开发者能够使用现代c++语言和一致的异步模型进行程序开发.
背景
大部分程序都需要与外界交互,可能通过文件、网络、或者串口.有时候,网络通信,单个i/o操作需要很长时间完成.这给应用程序开发带来了特殊的挑战.
Boost.Asio提供了管理这些耗时操作的工具,而不需要开发人员使用基于传统线程和显式锁的并发模型.
核心概念和功能
Boost.Asio剖析
Boost.Asio可用来执行同步和异步操作,如socket上的i/o操作.接下来,我们通过一系列概念图来理解Boost.Asio是如何工作的.
先来看一下执行同步连接时发生的操作:
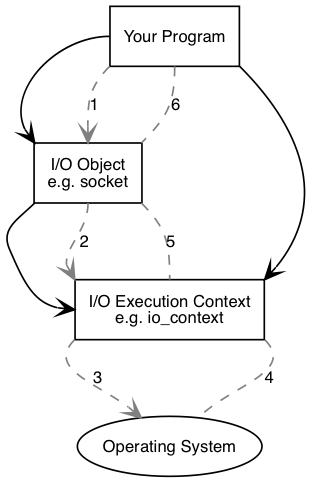
你的程序需要至少有一个io执行context,它是一个boost::asio::io_context、boost::asio::thread_pool、或boost::asio::system_context对象.这个io执行context将作为代理连接操作系统提供的io服务.
1 | boost::asio::io_context io_context; |
然后你的程序需要一个类似tcp socket的i/o对象来执行i/o操作.
1 | boost::asio::ip::tcp::socket socket(io_context); |
同步操作
执行了同步连接操作之后,下列事件会依次发生:
- 调用
i/o对象初始化连接操作
1 | socket.connect(server_endpoint); |
i/o对象将操作交给i/o执行contexti/o执行context调用操作系统接口执行连接操作- 操作系统将
i/o执行结果返回给i/o执行context i/o执行context将操作的错误信息转换为boost::system::error_code.error_code可与特定值进行比较,或者测试其真值(false意味着没有错误).然后将执行结果传递回i/o对象.- 如果操作失败,
i/o对象抛出boost::system::system_error异常.如果操作以下面接口调用:
1 | boost::system::error_code ec; |
那么则不会抛出异常,并且ec被设置为操作结果.
异步操作
执行了异步操作之后,将发生以下事件:

- 调用
i/o对象初始化连接操作
1 | socket.async_connect(server_endpoint, your_completion_handler); |
其中your_completion_handler有以下签名:
1 | void your_completion_handler(const boost::system::error_code& ec); |
执行不同异步操作的完成函数有不同的签名.
i/o对象将操作交给i/o执行contexti/o执行context通知操作系统需要执行异步连接.
时间流逝(在同步操作里,这个时间包含连接操作的全部时间).
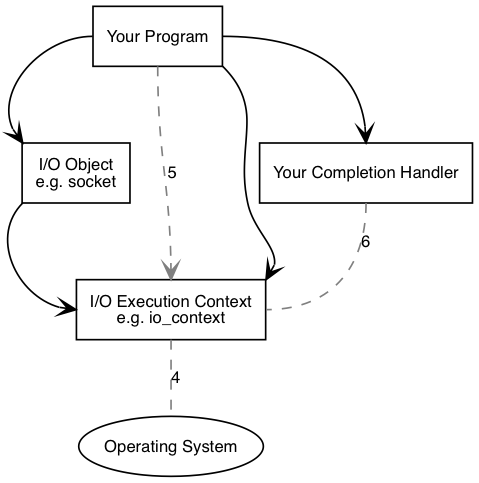
- 操作系统通过将执行结果放入一个队列来指示操作完成.这个结果可以被
i/o执行context取出. - 当使用
io_context作为i/o执行context时,你的程序必须调用io_context::run(或者其它类似的成员函数)以检索结果.io_context::run在有未完成的异步操作时会一直阻塞,所以你可以在开始第一个异步操作后就调用它. - 在
io_context::run内部,i/o执行context获取操作结果,将其转化为error_code,然后传递给异步完成回调函数.
Proactor模式:不使用线程的并发
Proactor和Boost
我们先看一下Proactor设计模式在Boost.Asio中的实现,其中不包含任何特定平台的细节:
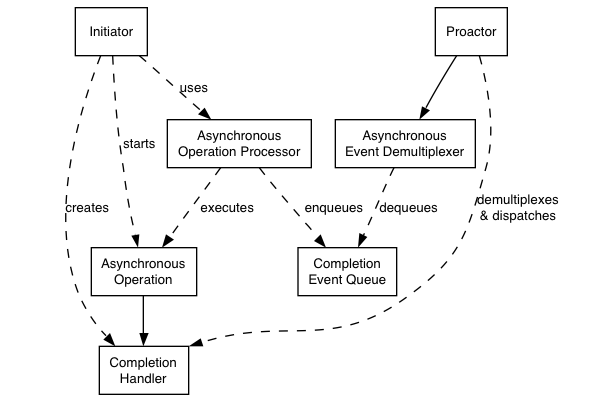
Proactor模式:
- 异步操作(Asynchronous Operation)
定义异步操作,比如:socket上的异步读/写.
- 异步操作处理器(Asynchronous Operation Processor)
执行异步操作并在操作完成时向异步事件完成队列中存入完成事件.从高层视角来看,内部服务如reactive_socket_service是异步操作处理器
- 事件完成队列(Completion Event Queue)
缓存完成事件,直到异步事件分发器从中取出事件.
- 完成处理句柄(Completion Handler)
处理异步操作结果.这些函数对象通常使用boost::bind创建.
- 异步事件解复用器(Asynchronous Event Demultiplexer)
阻塞直到完成事件队列有事件,然后将完成事件传递给调用者.
- Proactor
调用异步事件解复用器来读取事件,然后将其分发给相关事件的完成处理句柄(比如.调用函数对象).这是io_context类所代表的抽象.
- 初始化
应用程序通过高层的接口如basic_stream_socket启动特定的异步操作,这个接口将其代理给reactive_socket_service.
使用Reactor来实现
在很多平台上,Boost.Asio使用Reactor来实现Proactor模式,这些Reactor可能是select,epoll或kqueue
- 异步操作处理
reactor使用select,epoll或者kqueue实现.当reactor表明资源已经就绪,处理器执行异步操作并将相关的完成处理函数加入完成事件队列中.
- 完成事件队列
完成处理句柄(如函数对象)的链表.
- 异步事件分发器
通过事件或条件变量在完成事件队列上等待完成句柄可用.
在windows上使用overlapped I/O
优势
可移植
由Boost.Asio选择最合适的异步机制,如Windows上使用原生的异步I/O api,而在POSIX上使用epoll、select.并发与线程解耦
长时间的操作可以异步执行,因此程序不需要通过创建大量线程来提高并发度.高性能和可扩展
使用异步操作有可能通过减少线程数量来避免过多的上下文切换开销,数据间同步和移动.简化同步
异步处理可以在一个线程中完成,应用程序逻辑可以较少的关注同步问题.函数组合
函数组合是指实现一个高层次操作的的函数,如以特定格式发送一个消息.每个函数都有可能多次调用底层读/写操作来实现.
比如,考虑如下一个协议:每条消息由一个定长的消息头和一个可变的消息体构成.消息体的长度在消息头中指定.一个可能的read_message操作可以使用两次低级read实现,第一次用于接收消息头并获取长度,第二次接收整个消息体.
可以用异步方式组合函数功能,异步操作可以进行链式连接.一个操作完成后可以初始化下一步操作.通过将这些操作封装到首次操作中,调用者感受不到高层操作是通过异步调用链实现的.通过组合操作的能力,可以更容易开发具有高级抽象的网络库,用于支持特定的协议.
劣势
编程复杂
由于异步操作的初始化和完成在时间和空间上是分散的,因此编程更为复杂.另外,由于控制流的颠倒,应用程序的调试也会变得困难.内存开销
缓冲区必须持续存在于读/写操作期间,这可能会持续不确定的时间,另外每次并发操作都需要单独的缓冲区.而Reactor模式,在socket就绪前不需要缓冲区用于读或写.
线程和Boost.Asio
线程安全
通常,并发地使用不同对象是安全的,但是并发地使用同一个对象是不安全的.但是,io_context提供了强保证,并发地使用其单一对象是安全的.
线程池
可以让多个线程调用io_context::run来使用线程池执行完成事件.这种方法还可以与post()方法一起使用作为在线程池间执行任意计算任务的方法.
注意所有调用io_context::run的线程是等价的,io_context可能以任意顺序分配任务.
内部线程
库的内部实现可能使用内部线程来模拟异步.这些线程应该尽可能地对用户不可见.另外,这些线程必须做到:
- 不直接调用用户代码
- 必须阻塞所有信号
这一方法得到了以下保证:
- 异步完成处理函数只在调用
io_context::run的线程中调用
因此,库的使用者有责任创建和管理所有线程及通知由哪个线程处理.
这种设计的原因有:
- 通过在唯一的线程中调用
io_context::run(),用户代码可以避免同步的复杂性. - 库的使用者可能需要在线程启动时执行一些初始化操作.如
COM的CoInitializeEx - 库的接口与线程创建和管理接口解耦,允许在不支持线程的平台上执行.
Stands: 在线程中使用无锁操作
strand被定义为严格地按顺序执行事件的处理函数.使用strand允许在多线程程序中执行代码而不需要显式的使用锁(比如,使用mutexes).
strand可以显式或隐式的使用,下面描述了几种方式:
- 在唯一的线程中调用
io_context::run(),这样所有的事件处理操作会隐式的串行执行,因为io_context保证所有的操作都在run()中执行. - 同一个
connection上关联的异步操作链(eg.一个半双工HTTP实现),异步操作不可能并发地执行.这也是隐式的strand. - 显式的
strand是一个strand<>或io_context::strand的实例.所有的事件函数对象需要通过使用boost::asio::bind_executor()绑定到strand,或者通过strand对象的posted/dispatched方法.
在组合异步操作的情况下,比如async_read()或async_read_until(),如果完成handler使用了strand,那么所有的间接操作也需要使用同样的strand.这是为了保证所有调用者和组合操作之间共享的任意对象的访问是线程安全的.(比如在socket上使用async_read,调用者可以进行close操作).
为了达到这种效果,所有的异步操作可以通过get_associated_executor函数来获取handler相关的executor.比如:
1 | boost::asio::associated_executor_t<Handler> a = boost::asio::get_associated_executor(h); |
相关的executor必须满足Executor的要求.它将被异步操作用来提交执行间接或者最后的handlers.executor可以被特定的handler进行定制化,通过指定一个内嵌的type executor_type和成员函数get_executor():
1 | class my_handler |
对于更复杂的情况,可以直接定制化associated_executor模板:
1 | struct my_handler |
boost::asio::bind_executor()函数可以用来帮助绑定一个指定的executor对象,比如一个strand到完成handler.这种绑定自动关联一个上面展示的executor.比如,为了绑定一个strand我们可以像下面这样:
1 | my_socket.async_read_some(my_buffer, |
无栈协程
coroutine类提供了对无栈协程的支持.无栈协程可以用同步的方式实现异步逻辑,而且开销很小.
下面是一个例子:
1 | struct session : boost::asio::coroutine |
coroutine类与伪关键字reenter,yield和fork结合起来使用.它们是预编译宏,使用了与Duff装置相似的技术.
有栈协程
spawn()函数是运行有栈协程的一个高层接口.
下面是示例代码:
1 | boost::asio::spawn(my_strand, do_echo); |
spawn()的第一个参数可以是strand,io_context或者completion handler.这个参数决定了协程可以执行的context.比如,一个服务的每个客户对象可能由多个协程组成;它们应该运行在相同的strand上,这样就不需要额外的同步操作.第二个参数是一个具有如下签名的函数对象:
1 | void coroutine(boost::asio::yield_context yield); |
用于指定协程将要执行的代码.参数yield可以在需要的时候作为completion handler传递给一个异步操作,比如:
1 | std::size_t length = |
上面的代码开启了一个异步操作并将当前协程挂起,协程将会在异步操作完成后继续执行.
异步操作的handler签名如下:
1 | void handler(boost::system::error_code ec, result_type result); |
初始函数返回result_type.在上面的async_read_some例子中,是size_t.如果异步操作失败,error_code会转换成system_error异常并抛出.
对应的handler签名如下:
1 | void handler(boost::system::error_code ec); |
要收集error_code而不抛出异常,可以向下面代码那样关联输出到yield_context:
1 | boost::system::error_code ec; |
注:如果对spawn()使用定制的Handler类型,函数对象的原型如下:
1 | void coroutine(boost::asio::basic_yield_context<Handler> yield); |
支持协程TS
通过awaitable类模板,use_awaitable完成标识和co_spawn()函数来支持协程TS,这些工具结合使用co_await关键字可以使开发者以同步的方式实现异步操作.
1 | boost::asio::co_spawn(executor, |
co_spawn()的第一参数是允许coroutine执行的executor.比如,一个服务的某个客户端对象可能包含多个协程;为了避免额外的同步操作,它们需要运行在同一个strand.
第二个参数是一个返回值为boost::asio::awaitable<R>的函数对象,R是coroutine的返回值,在上面的例子中是void.
第三个参数是一个完成标识,co_spawn()用它来创建签名为void(std::exception_ptr, R)的完成函数.当协程运行完成时,完成函数会用协程的返回值来调用.上面的例子中是boost::asio::detached,代表忽略协程的返回值.
在上面的例子中,协程体由echo函数实现.当向异步操作传递use_awaitable完成标识时,异步操作的返回值可以使用co_wait关键字来获取:
1 | std::size_t n = co_await socket.async_read_some(boost::asio::buffer(data), boost::asio::use_awaitable); |
异步操作的handler有如下签名:
1 | void handler(boost::system::error_code ec, result_type result); |
这时co_wait表达式的返回类型就是result_type.上面的async_read_some的返回值是size_t,如果异步操作失败,error_code会转换为system_error异常并抛出.此时handler签名为:
1 | void handler(boost::system::error_code ec); |
此时co_wait产生一个void返回值.对于上面例子来说,错误以system_error异常的形式传递给协程.